|
Si tiene instalado el programa Amanuense, podrá
ver correctamente escrita la transliteración que contienen estas páginas. De
lo contrario, puede utilizar la siguiente tabla:
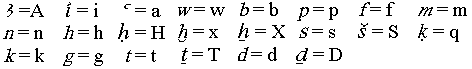
Puede
encontrar éste y muchos más textos traducidos y comentados por Ángel
Sánchez Rodríguez, en su libro "La Literatura en el Egipto Antiguo
(Breve antología)", editado por Egiptomanía S.L. Las traducciones
de esta web son más literales, en el libro pueden comprenderse mejor:

El
papiro matemático Rhind
Título
60.11. iw
isT grt spXr.n.tw Sfdw pn m HAt-sp (Hsbt) 33 Abd 4 Axt
Es ahora cuando se ha registrado este
rollo de papiro en el año de reinado 33, el cuarto mes de la estación del
‘ajet’
60.12. xr
Hm n nsw-bit aA-wsr-ra d anx
m-snt r Ssw n iswt
bajo la majestad del rey del Alto y Bajo
Egipto Aauserra ¡dotado de vida! en concordancia con los escritos de los
antiguos
60.13.
iry m-hAw nsw-bit n-mAat-ra in sS iaH-
que fueron hechos en el tiempo del rey del
Alto y Bajo Egipto Enmaatra por el escriba Ah-
60.14.
-msw spXr
snn pn
-mosu
quien registró este papiro.
Problema 26
60.15. aHaw
r-4.f Hr.f xpr.f
m 15 wAH-tp m 4
Una cantidad y su cuarto sobre ella se
convierten en 15. Se toma como 4
60.16. ir.xr.k
r-4.sn m 1 dmD 5 wAH-tp m 5 r gmt
y entonces se obtendrá su cuarto en 1. En
total 5. Se dividirá entre 5 para encontrar
60.17. 15
sxp.xr 3 wAH-(tp) m 3 spw 4
xpr.xr 12 r-4
3
15 y entonces se transformará en 3. Se
multiplicará 3 por 4 y se convertirán en 12. Un cuarto, 3.
60.18. dmD
15 aHaw 12 r-4.s 3
dmD 15
En total 15. La cantidad es 12, su cuarto
es 3. En total 15.
Problema 36
60.19.
iw.i hAA.kwi spw 3 (r HqAt)
r-3.i r-5.i Hr.i iw.
Descendí
3 veces con una medida de heqat [con] 1/3 mío, 1/5 mío sobre lo mío. Volví
60.20. mH.kwi
pty pA aHaw Dd sw
habiendo[lo] llenado
¿Cuál es la cantidad que se ha dicho?.
Problema 41
60.22. tp
n irt SAa pXr n 9 10 xb.xr.k
r-9 n 9 m 1
Ejemplo de hacer un contenedor circular de
9 unidades [de diámetro] y 10 unidades [de altura]. Entonces restarás 1/9 de
9, o sea una unidad [del total]
60.23. DAt
8 wAH-tp m 8 r
spw 8 xpr.xr 64 ir.xr.k
quedando 8. Luego multiplicarás 8 por 8 y
se convertirá en 64. A continuación realizarás
61.1. wAH-tp
m 64 r sp(w) 10 xpr.xr.f
m 640 d gs.f
la multiplicación de 64 por 10 y se
convertirá en 640. Debes colocar su mitad
61.2. Hr.f
xpr.xr.f m 960 rxt.f m XArw
sobre él y se convertirá en 960, su
cantidad en ‘jaru’.
61.3. ir.xr.k
r-20 n 960 m 48 hAAwt
pw r.f m HqAt
A continuación harás 1/20 de 960 en 48.
Esto es lo que desciende, pues, en heqat.
61.4. sSrw
48 HqAt qi n
sSmt.f
Grano: 48 heqats. Forma de su control
(prueba).
Problema 51
61.6. tp
n irt spdt m AHt mi
Dd n.k spdt nt
Ejemplo de hacer un triángulo de área
como se te dice. Un triángulo de
61.7. xt
10 Hr mryt.s xt 4
m tp-r.s pty
Aht.s ir.t(w) mi
10 jet en su altura y 4 jet en su base. ¿Cuál
es su área? Se hace como
61.8. xpr
ir.xr.k g n 4 m 2
r rdt ifd.s ir.xr.k wAH-
sigue: entonces harás la mitad de 4 en 2
para conseguir su rectángulo. A continuación harás la multiplicación
61.9.
-tp m 10 r sp(w) 2
AHwt.s pw
de 10
por 2. Esta es su área.
61.10.
1
400
1
1000
61.11.
1/2
200
2
2000
AHwt.s pw 20
Problema 62
61.12.
tp n irt qrft Xr aAt aSAt
mi Dd n.k qrft
Ejemplo de hacer un saco portando
abundantes minerales como se te dice. Un saco
61.13. nbw
im.s HD im.s DHty im.s iw
in.tw qrft
con oro en él, plata en él y plomo en él.
Se trae el saco
61.14.
tn Hr Saty 84 pty
ntt n aAt nbt
este con 84 shatys. ¿Qué hay de cada
mineral?.
61.15. iw
ir ddt Hr nbw dbn Satw
12 pw HD dbn
En cuanto a lo que se da en oro, el deben
son 12 shatys, [en] plata, el deben
61.16. Satw
6 pw DHty dbn Satw 3 pw
dmD.xr.k ddwt
son 6 shatys, el deben son 3 shatys.
Entonces sumarás lo que se da
61.17. Hr
dbn n aAt nbt xpr.xr
21 ir.xr.k pA 21
en debenes de cada mineral y se convertirán
en 21. A continuación harás que 21
61.18.
r gmt Satw 84 inyt
pw m qrft tn
divida a 84. Esto es lo se trae en este
saco.
61.19. xpr.xr
m 4 dd.k n aAt
nbt ir.t(w)
mi xpr ir.xr.k
y se convertirá en 4 que colocas de cada
mineral. Se hace como sigue: entonces harás
61.20. wAH-tp
m 4 r spw 12 xpr.xr
nbw m 48 rxt.f pw
la multiplicación de 4 por 12 y se
convertirá el oro en 48. Esta es la lista.
61.21.
6
HD
24
61.22.
3
DHty
12
61.23.
21
dmD
84
Problema 65
62.1.
tp n irt tw 100 n s 10 TAw Tsw iry-aA
Ejemplo para hacer 100 panes para 10
hombres: un patrón, un comandante y un portero
62.2. m-qAb
sSmt.f dmD.xr.k nA n rmT
apr
[recibiendo] el doble. Su resultado.
Entonces totalizarás los hombres que deben suministrarse
62.3. xpr.xr
13 wAH-tp m 13 r
gmt tA tw 100 xpr.xr
y se convertirán en 13. Dividirás entre
13 los 100 panes y se convertirá
62.4. 7
2/3 r-39 Dd.xr.k wnm pw n pA 7
TAw
en 7 2/3 1/39. Entonces dirás: ‘esta es
la ración de los siete hombres’, el patrón,
62.5.
Tsw iry-aA m-qAb
el comandante y el portero, el doble.
62.7.
15 r-3 r-26 r-78
15 1/3 1/26
1/78
Problema 67
62.8.
tp n Hsb bAkw n mniw
ist grt iy.n mniw
Ejemplo de hacer el recuento de las tasas
de un vaquero. Cuando hubo venido el vaquero
62.9. pn
r irw Xr kAw 70 Dd.n
nisw pn n kAw
este en relación con las tasas portando
70 toros, dijo este recaudador de los toros
62.10. n
mniw pn and.wy
xtmw in.k
iw tr Tnw
a este vaquero: ‘Que poca es la tasa de
ganado de traes. Ciertamente debe de ser la cantidad
62.11. xtmw.k
aSAw Dd.n mniw pn
xr.f in.i n.k
de tu tasa de ganado mayor’.
Dijo este vaquero a él: ‘Te traigo
62.12. m
2/3 n r-3 n kAw sip.n.k
n.i Hsb.n.i gm.kwi
de los 2/3 del tercio de los toros que me
has asignado. He hecho recuento habiendo encontrado
62.13. km.kwi
ir.t(w) mi xpr
· · · 2/3
n r-1/3.f m r-6 r-18
y totalizado. Se hace como sigue: los 2/3
de su tercio [se convierten] en 1/6 1/18.
62.14. nis.xr.k
xnt r-6 r-18
1
r-6 r-18
A continuación se llamara lo que está
fuera r-6 r-18. # 1 1/6
1/18
62.15. ir.xr.k
wAH-tp m 70 r spw 4 1/2
2
r-3 r-9
En consecuencia harás la multiplicación
de 70 por 4 1/2, # 2 1/3 1/9
62.16. xpr.xr
315 nA pw sipy
n.f 4
2/3 r-6 r-18
y se convertirá en 315. Esto es lo que se
le ha asignado. # 4 2/3
1/6 1/18
62.17.
1
135
2/3 n r-3.f 70 1/2
1/9
62.18.
2/3
120
nA pw in.f dmD
1
62.19. r-3.f
105
|